应用密码学总结

绪论

密码学发展历史

古代加密方法（手工阶段）

古典密码（机械阶段）

近代密码（计算机阶段)

网络信息安全的机制和安全服务

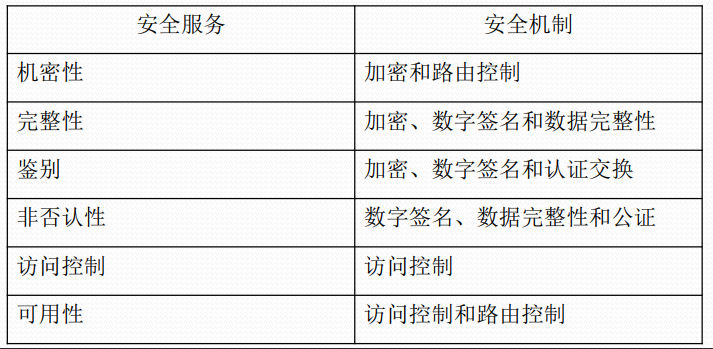
image-20231220191629472

安全攻击的主要形式及分类

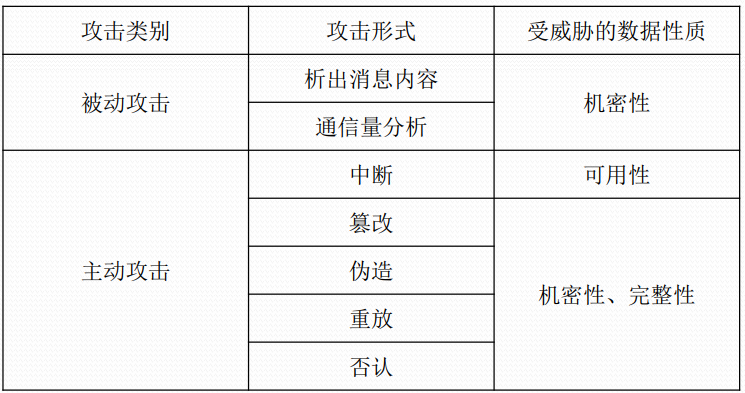
image-20231220191743077

密码学基础

密码学相关概念

密码学 (cryptology) ✓是密码编码学和密码分析学的统称

密码编码学(cryptography) ✓通过变换消息使其保密的科学和艺术 ✓是密码理论的基础，也是保密系统设计的基础

密码分析学(cryptanalysis) ✓在未知密钥的情况下从密文推演出明文或密钥的艺术

密码编码学和密码分析学既相互对立，又相互促进和 发展

密码分析分类：根据密码分析者对明文、密文等信息 掌握的多少

唯密文攻击 (Ciphertext-only Attack) ：破译者已知：密码算法、待破译的密文

已知明文攻击 (Known-plaintext Attack) ：破译者已知：密码算法、一定数量的明文-密文对、截获 的待解密的密文

选择明文攻击 (Chosen-plaintext Attack) ：破译者已知：密码算法、选定的明文和对应的密文

选择密文攻击 (Chosen-ciphertext Attack) ：破译者已知：密码算法、选定的密文和对应的明文

选择文本攻击 (Chosen-text Attack)：破译者已知：密码算法、选定的明文和对应的密文、选 定的密文和对应的明文

密码系统

密码体制的安全性仅应依赖于对密钥的保密，而不应依 赖于对算法的保密

密码系统的安全条件

计算安全性 指使用目前最好的方法攻破它所需要的计算远远超出攻击 者的计算资源水平，则可以定义这个密码体制是安全的

可证明安全性 这种方法是将密码系统的安全性归结为某个经过深入研究 的数学难题，数学难题被证明求解困难。 该方法存在的问题：只说明了安全和另一个问题是相关的 ，并未完全证明问题本身的安全性

无条件安全性 假定攻击者拥有无限的计算资源，但仍然无法破译该密码 系统。 除一次一密方案外，无其他的加密方案是无条件安全的。 一次一密方案使用与消息一样长的随机密钥，且密钥使用 永不重复。 但是不实用，因为消息发送者和接受者必须每次安全更新 随机密钥，在当前技术条件下这并不现实

密码系统用户所能做的全部努力就是满足下面准则中的 一个或两个

➢ 破译密文的代价超过被加密信息的价值

➢ 破译密文所花的时间超过信息的有用期

安全模型

密码体制

对称密码体制 非对称密码体制

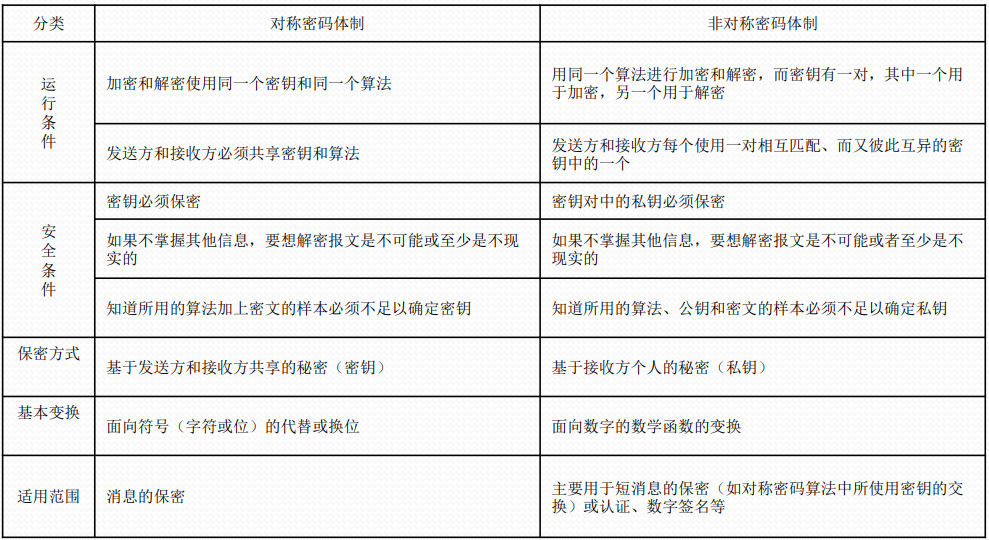
image-20231220193216627

古典密码

代替密码

单表代替密码和多表代替密码。

单表代替密码

移位密码

加密变换，E={E:Z26→Z26, Ek (p) = p + k (mod26)| p∈P, k∈K }

解密变换，D={D:Z26→Z26, Dk (c) = c－k (mod26)| c∈C, k∈K }

使用密钥的单表代替密码

设密钥为：spectacular。

明文： ABCDEFGHIJKLMNOPQRSTUVWXYZ

对应的密文：spectaulrbdfghijkmnoqvwxyz

仿射密码

仿射密码举例

✓ 设明文消息为China，密钥k = (k1 , k2 ) = (7, 3)，用仿射密 码对其进行加密，然后再进行解密。

✓ 解答：利用扩展的欧几里德算法可计算出k1 -1 = 7-1=15 (mod 26)，加密函数为Ek (p) = 7× p + 3 (mod 26)，对应 的解密函数为Dk (c) = 15 ×(c - 3) (mod 26)=15c-19 (mod 26)。

多表代替密码

**普莱费尔密码（Playfair Cipher） **

**维吉尼亚密码（Vigenere Cipher） **

希尔密码（Hill Cipher）

换位密码

密码的破解

单表代替密码攻击：统计分析攻击

多表代替密码的破解： Kasiski测试法， 重合指数法

数学引论

欧几里得算法

扩展欧几里得算法

费马定理

image-20231220205617568

欧拉函数

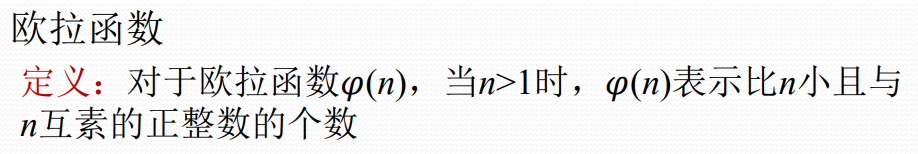
image-20231220210333547

image-20231220210347450

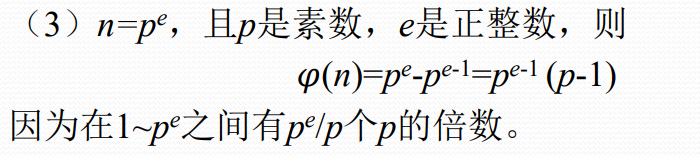
image-20231220210407592

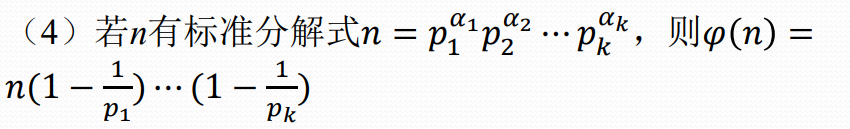
image-20231220210419371

欧拉定理

image-20231220210512517

对称密码体制——分组密码

针对安全性的分组密码设计要求

✓分组长度足够大

✓密钥量足够大

✓密码变换足够复杂

✓加密和解密运算简单，易于软件和硬件高速实现

分组密码的操作模式

img

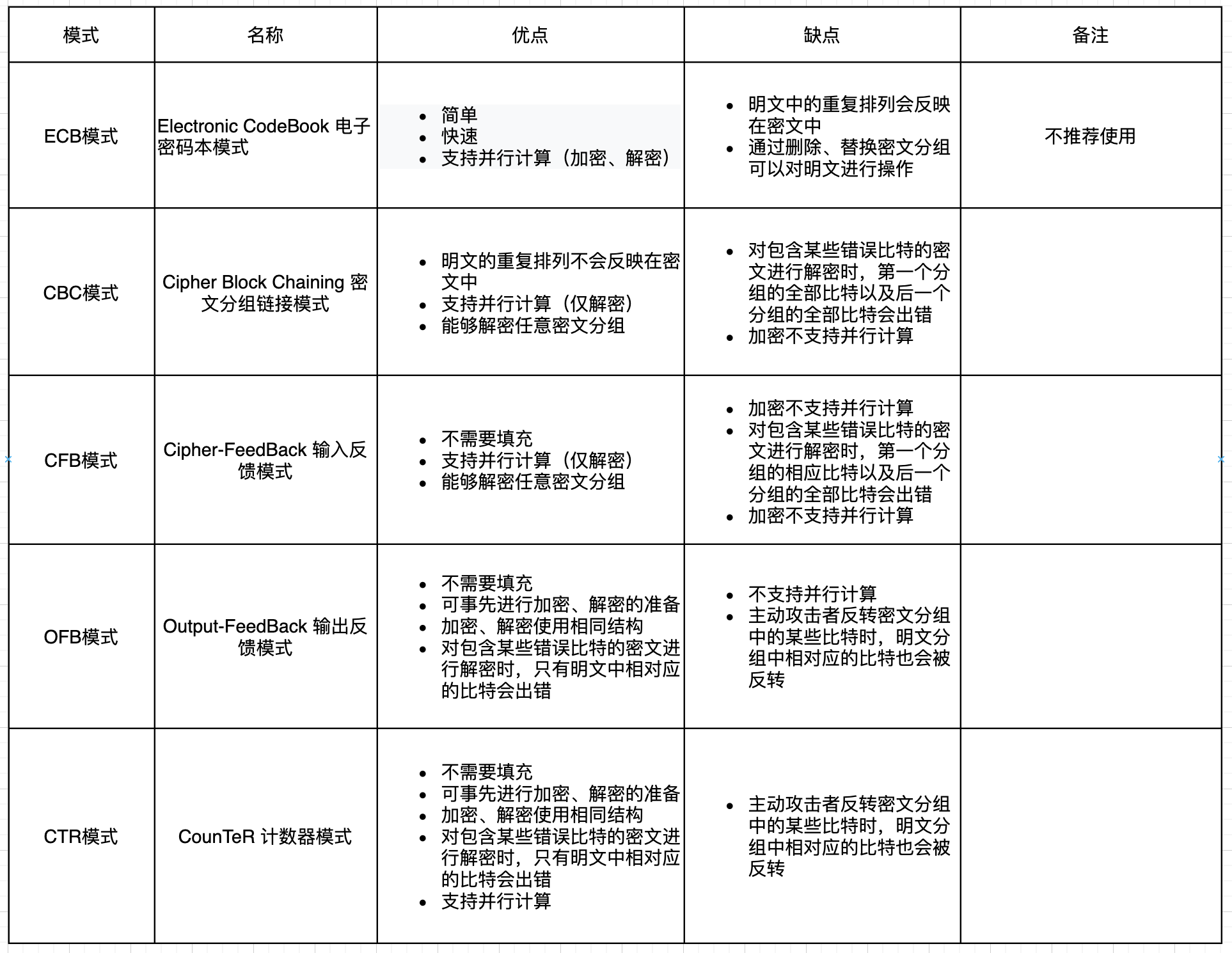
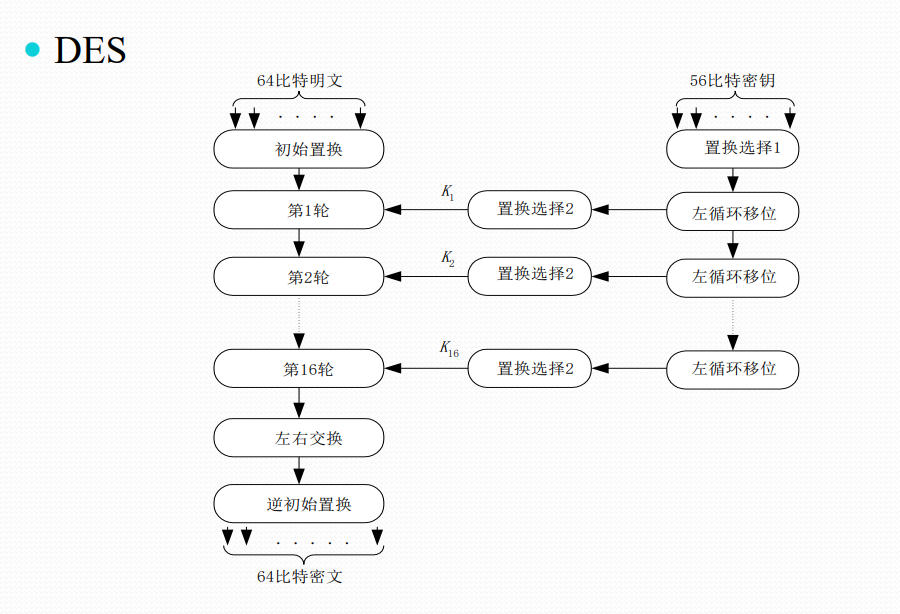
DES算法

1.明文分组64比特，使用的密钥为64位，有效密钥长度 为56位(有8位用于奇偶校验位或者完全随意设置)

2.DES由初始置换，16轮Feistel变换，逆初始置换组成

3.基本运算操作：置换、替换、异或与循环移位

image-20231221160220578

image-20231221160746276

AES算法

Rijndael算法是一种非Feistel密码结构的对称分组密码 体制，采用代替/置换网络

轮函数由3个不同的可逆均匀变换组成，称它们为3个 “层”：

✓线性混合层：确保多轮之上的高度扩散

✓非线性层：由16个S盒并置而成，起到混淆的作用

✓密钥加层：子密钥异或到中间状态

AES基本运算

✓字节代替SubBytes

✓列混淆MixColumns

✓轮密钥加AddRoundKey

✓行移位ShiftRows

非对称密码体制

概述

对称密码体制的主要问题

✓系统开放性差，需要可靠的密钥传递渠道

✓密钥管理困难 任何两个用户间要进行保密通信就需要一个密钥，不同用户 间进行保密通信时必须使用不同的密钥。n个用户需要 C(n,2)=n(n-1)/2个密钥，当用户量增大时密钥空间急剧增大。 如n=100时，C(100,2)=4995；n=500时，C(500,2)=124750

✓陌生人间的保密通信问题 对称密码体制的密钥分发方法要求密钥共享各方是互相信任 的

✓数字签名问题 对称密码体制不能实现通信中的抗抵赖需求

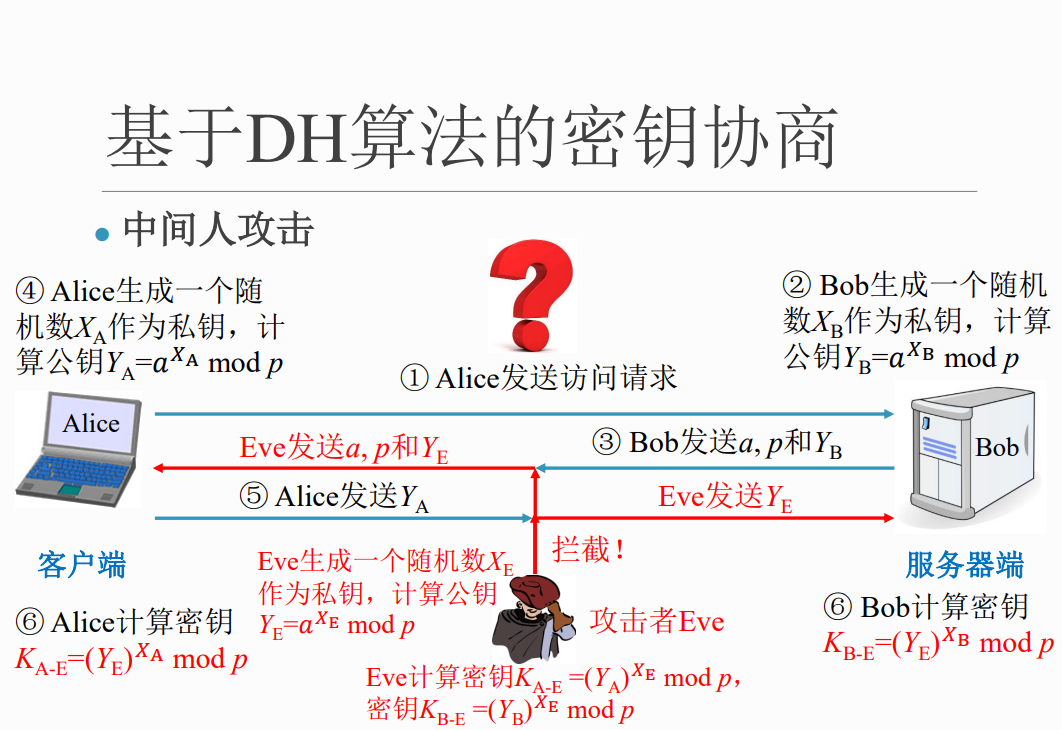
Diffie-Hellman密钥交换算法

算法的有效性依赖于计算有限域中离散对数的困难性

中间人攻击

image-20231221154325957

RSA

大整数的因子分解困难性

image-20231221154952339

如何快速计算a m mod n ：快速取模指数算法

如何检测一个数是素数 ：确定性素数测试算法，概率测试算法

如何找到足够大的素数p和q：确定性素数测试和概率测试结合

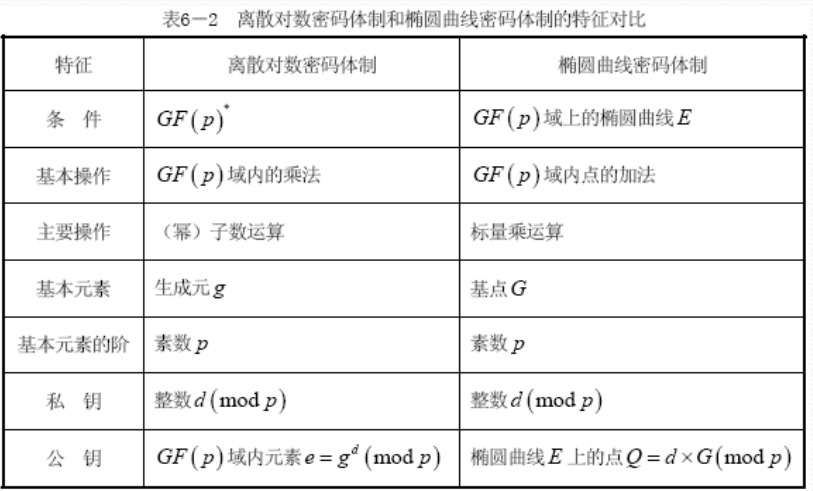
椭圆曲线密码体制ECC

ECC的安全性基于椭圆曲线离散对数问题的难解性

概念与定义

image-20231221162725036

image-20231221163259461

椭圆曲线的加法规则

image-20231221163350890

image-20231221163406983

image-20231221163535435

image-20231221164247854

image-20231221164430017

散列函数与消息认证

基本概念

✓消息认证用来抗击主动攻击

✓消息认证是一个过程，用于验证接受消息的真实性（的 确是由它所声称的实体发来的）和完整性（未被篡改、 插入、删除），同时还用于验证消息的顺序性和时间性 （未重排、重放、延迟）

✓除此之外，在考虑网络安全时还需考虑业务的不可否认性，即防止通信双方中的某一方对所传输消息的否认

✓实现消息的不可否认性可通过数字签名

✓数字签名也是一种认证技术，也可用于抗击主动攻击

✓消息认证机制和数字签名机制都有一产生认证符的基本 功能，这一基本功能又作为认证协议的一个组成部分

✓认证符是用于认证消息的数值，它的产生方法又分为消 息认证码（Message Authentication Code，MAC）、哈希 函数（Hash Function）两大类

消息认证码

系统实现功能

➢ 接收方相信发来的消息未被篡改

➢ 接收方相信发方不是冒充的image-20231221164819236

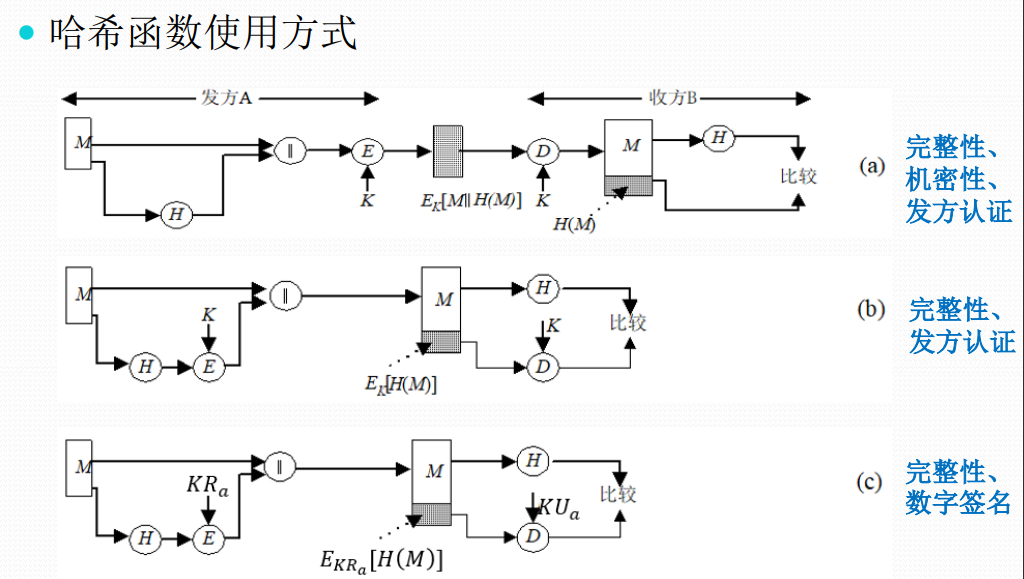
哈希函数

基本概念

✓又称杂凑函数或散列函数

✓哈希函数H可以将任意长度的消息M映射为**较短的、固定长度的一个值H(M)**，作为认证符

✓称H(M)为哈希值或哈希码或消息摘要

哈希函数性质

✓函数算法H公开

✓ 单向性：已知消息M，H(M)易于计算；但是已知H(M) ，求M计算不可行

✓ 弱抗碰撞性：已知消息M，找一个消息M’ (M’≠ M)，使 得H(M)=H(M’)计算不可行

✓ 强抗碰撞性：找出任意两个不同的输入M和M’，使得 H(M)=H(M’)计算不可行

✓ 雪崩性：微小修改消息M ，会使H(M)发生巨大变化

image-20231221165601184

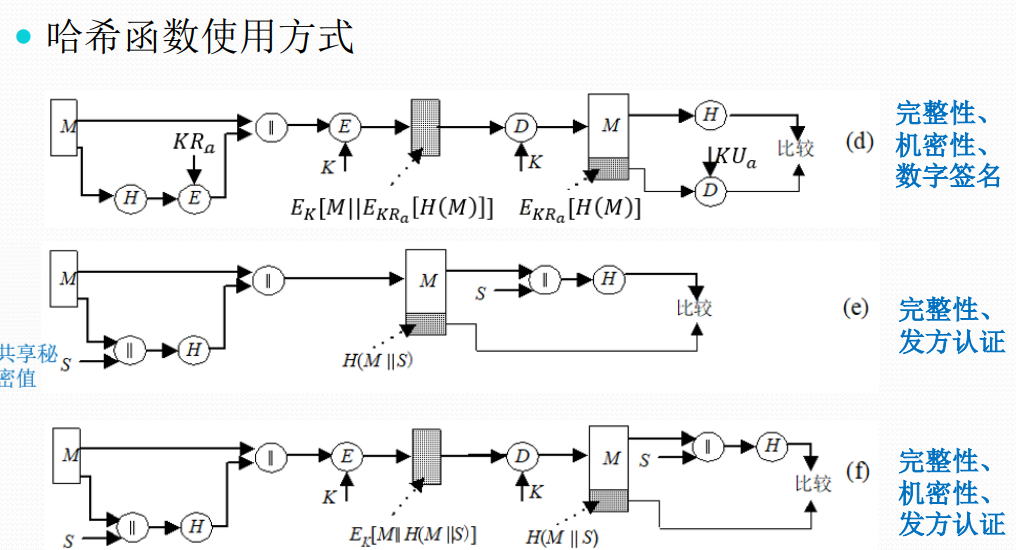
image-20231221165609636

数字签名

概述

数字签名是手写签名的一种电子模拟，针对电子文档 的一种签名确认方法

目的

✓用于向接收方或第三方证实消息被信源方签署

✓用于存储的数据或程序的完整性证实

数字签名性质

✓精确性：签名是对文档的一种映射，不同的文档内容所 得到的映射结果是不一样的

✓唯一性：签名应基于签名者的唯一性特征（如私钥）， 从而确定签名的不可伪造性和不可否认性

✓时效性：签名应该具有时间特征，防止签名的重复使用

数字签名要求

✓ 接收者能够核实发送者对报文的签名

✓ 发送者事后不能抵赖对报文的签名

✓ 接收者不能伪造对报文的签名

✓ 必须能够认证签名时刻的内容

✓ 签名必须能够被第三方验证，以解决争议

数字签名的产生方式（了解）

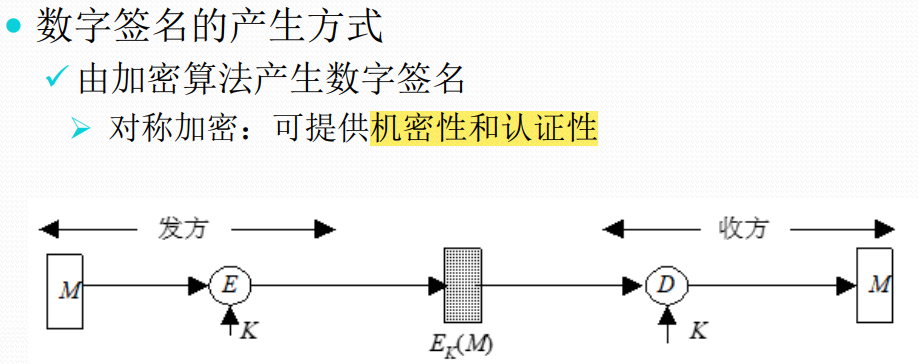
image-20231221170702137

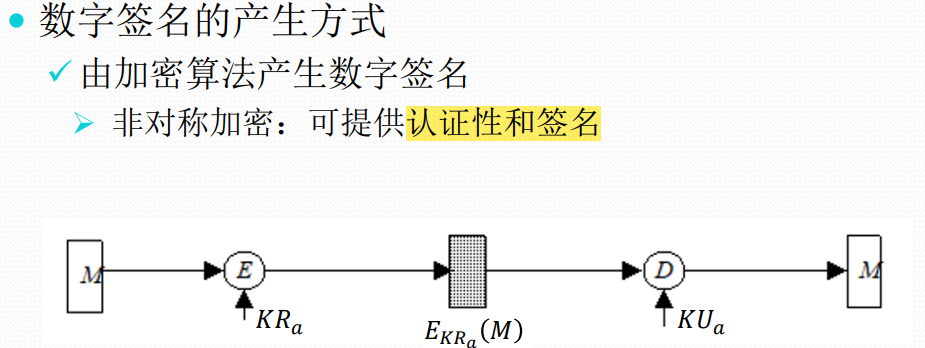
image-20231221170710815

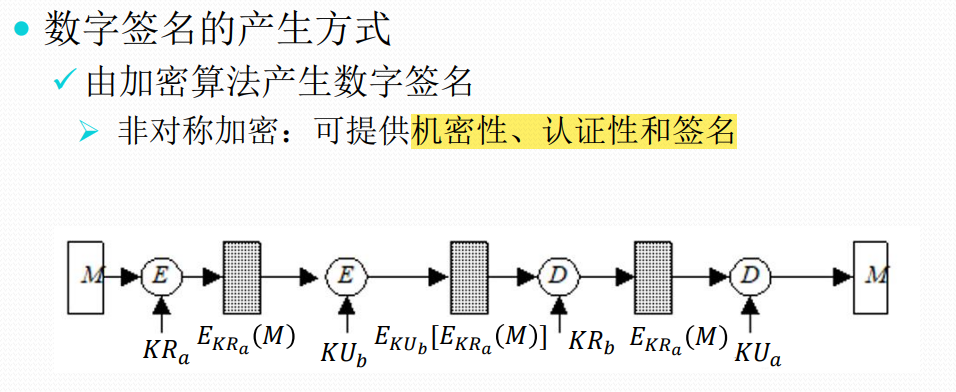
image-20231221170718329

RSA签名

image-20231221170736301

案例分析（大题）

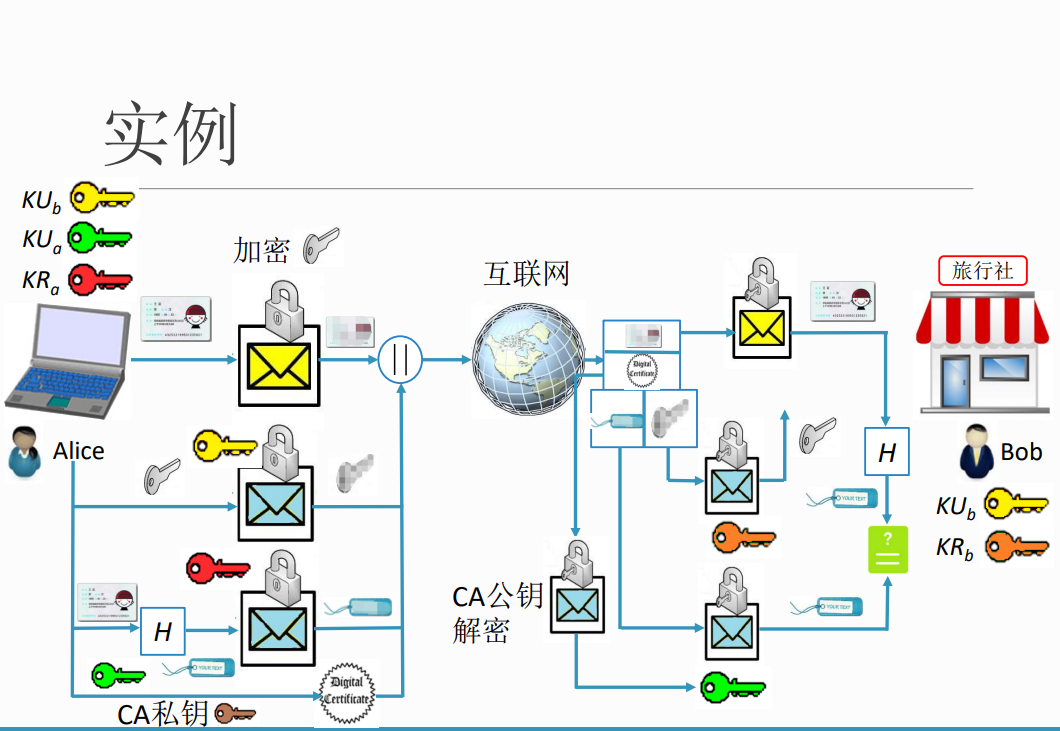
image-20231221171002379

密钥管理

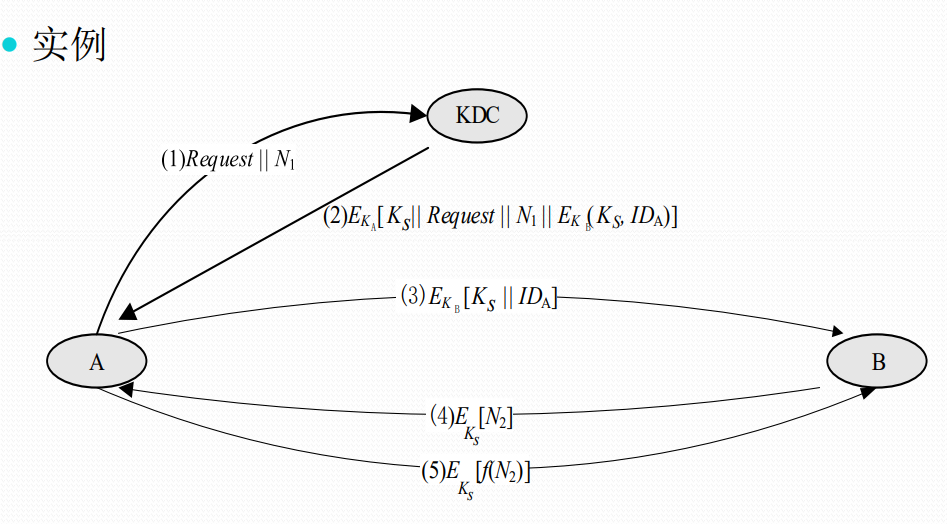
image-20231221171158455

公钥加密体制的密钥管理

公钥的分配方法——公用目录表

✓本方案的安全性虽然高于公开发布的安全性，但仍易受 攻击。如果敌手成功地获取管理员的秘密钥，就可伪造 一个公钥目录表，以后既可假冒任一用户又能监听发往 任一用户的消息，且公用目录表还易受到敌手的窜扰

公钥的分配方法——公钥管理机构

上述公钥管理机构分配公开钥时也有缺点，由于每一用 户要想和他人联系都需求助于管理机构，所以管理机构 有可能成为系统的瓶颈，而且由管理机构维护的公钥目 录表也易被敌手窜扰

序列密码

概念

序列密码，即流密码（Stream Cipher），按位或字节处理

序列密码与分组密码的区别

✓序列密码以一个符号作为基本的处理单元，而分组密码 以一定大小的分组作为基本的处理单元

✓序列密码使用一个随时间变化的简单的加密变换，即不同时刻所用的密钥不同，而分组密码在不同时刻所用的 密钥是相同的

序列密码分类

✓分为同步序列密码和自同步序列密码

✓在同步序列密码中，密钥流的产生与明密文消息流相互独立

同步序列密码

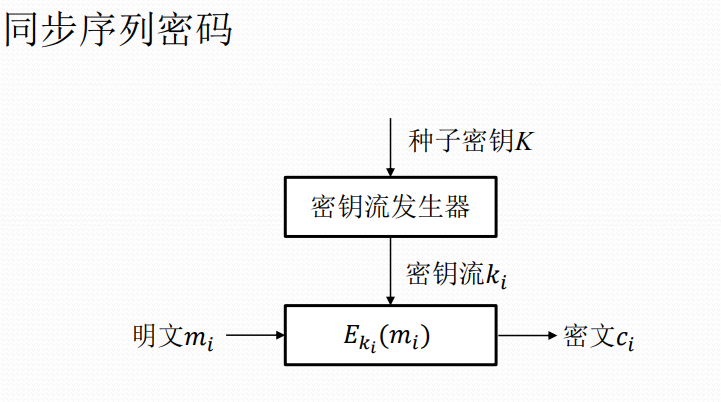
image-20231221171933113

同步序列密码特点

✓无错误传播，一个传播错误只影响一个符号，不会影响 到后继的符号 ✓同步要求

➢ 发送方和接收方必须保持精确的同步，用同样的密钥并作 用在同样的位置上，接收方才能正确的解密

➢ 通信中丢失或增加了一个密文字符，接收方将一直错误， 直到重新同步为止，这是同步序列密码的一个主要缺点

➢ 但对应的同步序列密码也能够容易检测插入、删除等主动攻击。这是因为一旦这种攻击发生，接收方就会出现解码 错误

自同步序列密码

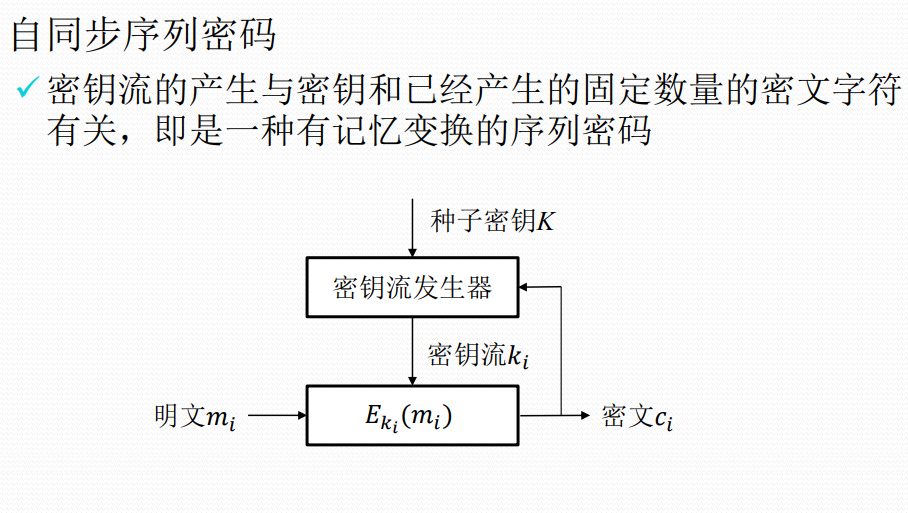
image-20231221172152791

自同步序列密码特点

✓有限错误传播

➢ 设自同步序列密码的密钥序列产生器具有n位存储，则一个 符号的传输错误将影响到后面n符号的解密，但不影响后面 第n+1个及其以后符号的解密

密钥流发生器设计准则

✓密钥量足够大（应不小于128位）

✓加密序列的周期足够长（一般为2 128或2 256）

✓密钥流应该尽可能地接近于一个真正的随机数流的特征

线性反馈移位寄存器（LFSR）可能有大题

求周期2的n次方减1

image-20231221202311569

#信息安全课程
应用密码学总结
http://example.com/2023/12/25/应用密码学总结/
作者
Sanli Ma
发布于
2023年12月25日
许可协议